로그(log)란 무엇인가?

로그함수는 지수함수의 역함수이며, 대수함수라고도 하고, log라는 기호를 사용한다.

로그는 실수 영역으로 확장된 지수에서 등장하는 새로운 무리수 개념이다.

# 로그의 뜻

로그는 지수를 표현하기 위해서 만들어졌다. 

예를 들어, 2를 몇제곱해야 8이 될까? 3제곱해야 8이 된다. (2³=8) 그리고 2는 4제곱해야 16이 된다. (2⁴=16)

그렇다면 2를 10으로 만드는 지수는 몇일까? 3보다는 크고 4보다는 작은 수이다.

그 수를 표현할 수 없어서 로그로 log₂10이라고 표현하기로 했다.

즉,  log₂10은 2에 붙여서 10을 만드는 지수가 되는 것이다.

x = log_ab 를 정의하자면, a를 b로 만드는 지수는 x라는 것이다.

# 로그의 조건

로그 바로 옆에 오는 아랫첨자의 작은 수는 '밑'이라고 표현하고, 옆에오는 큰 숫자는 '진수'라고 표현한다. 

여기의 수는 모두 조건이 있다. 로그는 지수의 표현이므로 지수의 조건이 따라오는 것이다.

 

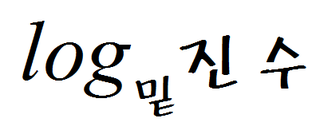
log_ab

i) 밑조건 : 밑은 1이 아닌 양수(a≠1, a>0)

ii) 진수조건 : 양수(b>0)

※ 밑에 1이 오게 되면 성립하지 않게 된다. 예를 들어, log₁5는 1에 붙여서 5를 만드는 수인데, 그런 수는 존재하지 않는다. 

따라서, 밑과 진수조건은 수학적으로 의미가 있는 최소한의 조건이다.

# 상용로그 의미

일반적으로 숫자는 10진법을 사용한다. 로그의 밑은 진법과 관련이 있기 때문에, 밑이 10인 로그를 제일 많이 사용한다.

일반적인 숫자에서 10진법이라는 것을 생략하는 것처럼 상용로그의 밑이 10일 경우 밑을 생략해도 된다.

# 상용로그 값

i) 진수가 10의 거듭제곱

진수가 10의 거듭제곱 일 때, 상용로그의 값은 정수가 되며 로그의 성질을 이용하여 간단하게 구할 수 있다.

하지만 좀 더 신속하게 계산하기 위해서는 0의 개수만큼 정수가 나온다는 것만 기억하다.

(단, 1보다 크면 양수, 1보다 작으면 음수)

      ···

log1000 = 3​​

log100 = 2

log10 = 1

log1 = 0

log0.1 = -1

log0.01 = -2

log0.001 = -3​

       ···

​⇒ 진수의 자리수가 로그값의 정수부분에 영향을 준다.

⇒ 로그값의 정수부분은 진수의 자리수를 결정한다.​

​

ii) 진수가 10의 거듭제곱이 아닐 때

진수가 10의 거듭제곱이 아닐 때, 상용로그의 값은 무리수가 나오게 된다.

그러나 진수의 자리수만 보고 상용로그의 값은 예측할 수 있어야 한다. (자리수에 1을 뺀 값이 나온다.)

ex)

log1000 = 3​​

log999 = 2.xx

log500 = 2.xx

log101 = 2.xx​

log100 = 2

log20 = 1.xx​

log10 = 1

log6 = 0.xx​

log1 = 0

log0.55 = -0.xx ​

log0.1 = -1

log0.0684 = -1.xx​

log0.01 = -2

log0.003 = -2.xx​

log0.001 = -3​

 

역시나

​⇒ 진수의 자리수가 로그값의 정수부분에 영향을 준다.

(진수가 1보다 크면 상용로그값은 양수, 0과 1사이면 음수를 가진다.)

###################################################################

라는 지수함수가 있을 때, 그 역의 관계를 로그함수를 사용하여 로 나타낸다

 

: a를 몇(y)제곱해야 x가 되는가?

다음과 같은 지수 식을 보게 되면, 

같은 의미를 가지는 로그식으로 변환을 해 줄 수도 있을 것입니다.

-> x는 a를 밑으로 하는 N의 로그

-> a를 거듭제곱하여 N이 되게 하는 지수 x => 로그 a의 N

가장 흔한 밑의 값으로는 2, 10과 이 있다.

밑이 2인 로그 -> 이진로그(binary log) -> lb x로 표현

밑이 10인 로그 -> 상용로그(common log) -> lg x로 표현

밑이 e인 로그 -> 자연로그(natural log) -> ln x로 표현

밑이 없는 는 상용로그일 수도 있고 자연로그일 수도 있으니까 문맥에 따라 구별해야 한다.

# 참고 사이트

https://terms.naver.com/entry.nhn?docId=3536995&cid=58577&categoryId=58577

https://blog.naver.com/jihyoseok/221155205577

https://junhyuk7272.blog.me/220566139299

https://junhyuk7272.blog.me/220567977846